Aufgabe 1:
Bilden Sie die Ableitung der Funktion f mit f(x)=(5x+1)·sin(x2).
(2 VP)
Aufgabe 2:Gegeben ist die Funktion f mit
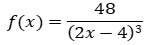.Bestimmen Sie diejenige Stammfunktion F von f mit F(3)=1.
(2 VP)
Aufgabe 3:Lösen Sie die Gleichung
.
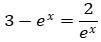(3 VP)
Aufgabe 4:Der Graph der Funktionen f mit
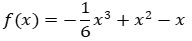besitzt einen Wendepunkt.Zeigen Sie, dass
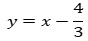eine Gleichung der Tangente in diesem Wendepunkt ist.
(4 VP)
Aufgabe 5: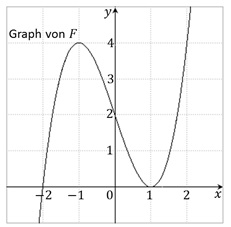
Die Abbildung zeigt den Graphen einer Stammfunktion F einer Funktion f. Entscheiden Sie, ob folgende Aussagen wahr oder falsch sind. Begründen Sie jeweils Ihre Entscheidung.
(1) f(1)=F(1)
(2)
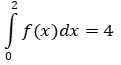
(3) f' besitzt im Bereich -1≤x≤1 eine Nullstelle.
(4) f(F(-2))>0
(5 VP)
Aufgabe 6:Gegeben ist die Gerade
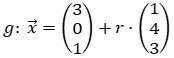.a) Untersuchen Sie, ob es einen Punkt auf g gibt, dessen drei Koordinaten identisch sind.
b) Die Gerade h verläuft durch Q(8|5|10) und schneidet g orthogonal.
Bestimmen Sie eine Gleichung von h.
(5 VP)
Aufgabe 7:Gegeben ist die Ebene E: 4x1+4x2+7x3=28.
Es gibt zwei zu E parallele Ebenen F und G, die vom Ursprung den Abstand 2 haben.
Bestimmen Sie jeweils eine Gleichung von F und G.
(3 VP)
Aufgabe 8:Bei einem Glücksrad werden die Zahlen 1, 2, 3 und 4 bei einmaligem Drehen mit folgenden Wahrscheinlichkeiten angezeigt:
| Zahl | 1 | 2 | 3 | 4 |
| Wahrscheinlichkeit | 0,4 | 0,1 | 0,3 | 0,2 |
a) Das Glücksrad wird einmal gedreht.
Geben Sie zwei verschiedene Ereignisse an, deren Wahrscheinlichkeit jeweils 0,7 beträgt.
b) An dem Glücksrad sollen nur die Wahrscheinlichkeiten für die Zahlen 1 und 2 so verändert werden, dass das folgende Spiel fair ist:
Für einen Einsatz von 2,50 € darf man einmal am Glücksrad drehen.
Die angezeigte Zahl gibt den Auszahlungsbetrag in Euro an.
Bestimmen Sie die entsprechenden Wahrscheinlichkeiten für die Zahlen 1 und 2.
(4 VP)
Aufgabe 9Von zwei Kugeln K1 und K2 sind die Mittelpunkte M1 und M2 sowie die Radien r1 und r2 bekannt. Die Kugeln berühren einander von außen im Punkt B.
Beschreiben Sie ein Verfahren, mit dem man B bestimmen kann.
(3 VP)